top of page

Brownian Motion:
Brownian motion B(t) is a stochastic process with the following properties:
-
B(t)-B(s) for t>s is independent of the past B(u) for s>=u.
-
B(t)-B(s) has Normal distribution with mean 0 and variance t-s. (Hence, B(t)~N(0,t))
-
B(t) is continuous
Examples of phenomena that appear to behave in this manner include stock market time-series data, particle motion, star motion within galaxies, etc.
Below we show some numerical simulations of Brownian motion in 1-dimension:
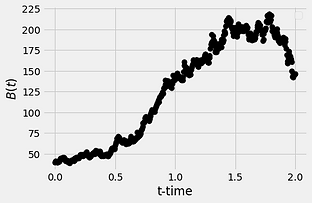
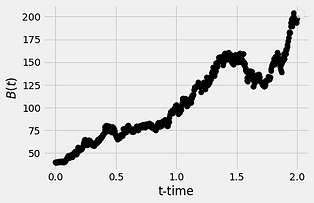
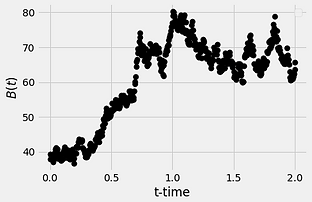
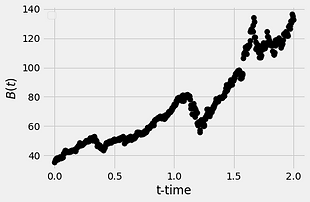
Actually, the figure on the bottom-right (very bottom, if you are viewing in mobile) is not Brownian motion. This figure is from the Stock-Market. As you can see, it appears as though we have simulated it using a computer. Now consider the following:

bottom of page